Insertion Sort in Cpp

Definition

Insertion Sort is basically insertion of an element from a random set of numbers, to its correct position where it should actually be, by shifting the other elements if required.

Insertion sort is a simple sorting algorithm that allows for efficient, in-place sorting of the array, one element at a time. By in-place sorting, we mean that the original array is modified and no temporary structures are needed.

Worst complexity: n^2
Average complexity: n^2
Best complexity: n
Space complexity: 1

Algorithm 
1. For k ← 2 to length [A]
2. Do key ← A[k]
3. i=k-1
4. while i>0 and A[i]>key
5. do A[i+1] ← A[i]
6. i=i-1
7. A[i+1] ← key

Program 

//Insertion Sort
#include<iostream.h>
#include<conio.h>
//Display Array
void display_array(int array[],int size){
int len = size;
for(int i=0;i<len;i++){
int val = array[i];
cout<<val;
(i==len-1)? cout<<".":cout<<",";
}
}
//Insertion Sort
void insertionSort(int array[],int size) {
for (int step = 1; step < size; step++) {
int key = array[step];
int j = step-1;
// Compare key with each element on the left of it until an element smaller than
// it is found.
// For descending order, change key<array[j] to key>array[j].
while (j >= 0 && key < array[j]) {
array[j + 1] = array[j];
--j;
}
array[j + 1] = key;
}
}

void main(){
clrscr();
int size = 8;
int array[10]={45,65,55,75,12,59,89,49}; // Array
cout<<"\n ------Insertion Sort------";
cout<<"\n Before Sorting \n";
display_array(array,size);
cout<<"\n After Sorting \n";
//Sort
insertionSort(array,size);
display_array(array,size);
getch();
}

Output

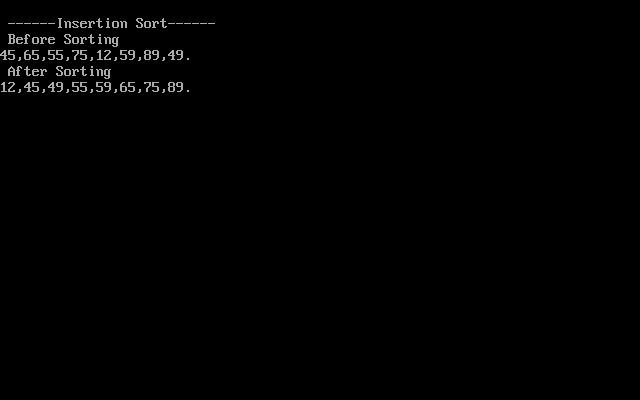
45,65,55,75,12,59,89,49.

12,45,49,55,59,65,75,89.

Space Complexity Analysis-

• It performs all computation in the original array and no other array is used.
• Selection sort is an in-place algorithm.

Important Notes-

• Insertion sort is not a very efficient algorithm when data sets are large.
• This is indicated by the average and worst case complexities.
• Insertion sort is adaptive and number of comparisons are less if array is partially sorted.

Live Demo